統計分布のグラフ
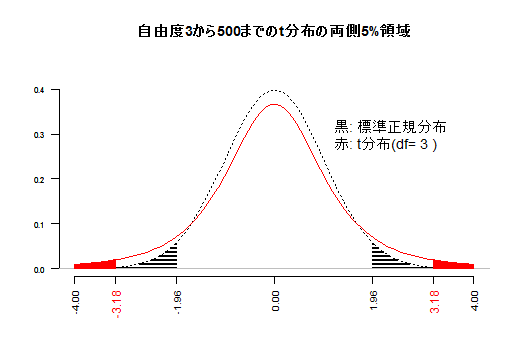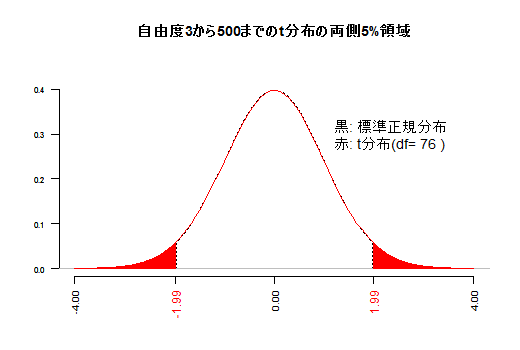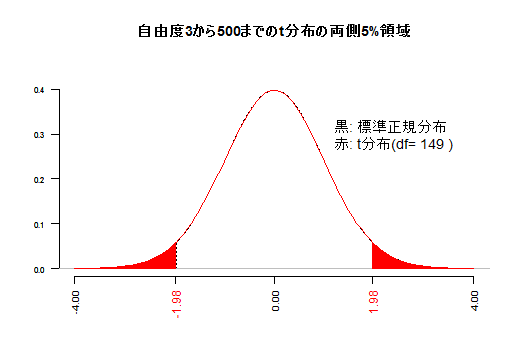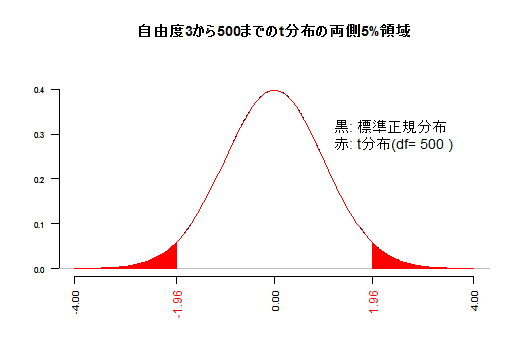
RとGiamで作成しました。それぞれのグラフをgif動画で見るにはグレーのタイトル領域の文字をクリックして下さい。再度クリックするとgif動画は非表示になります。(a) 自由度によって変化するt分布と,標準正規分布
t分布は標準正規分布を上から押し潰した形をしています。頂点が低く,裾が厚くなります。95%領域などは左右にはみ出します。自由度1と2は潰れ過ぎていて同じ横軸範囲で描画しにくいので,自由度3からとしています。
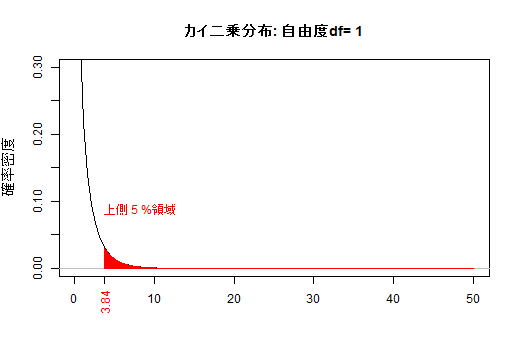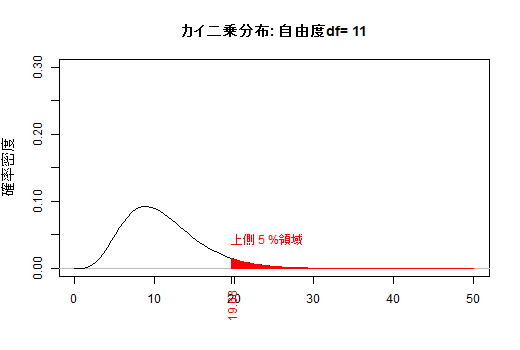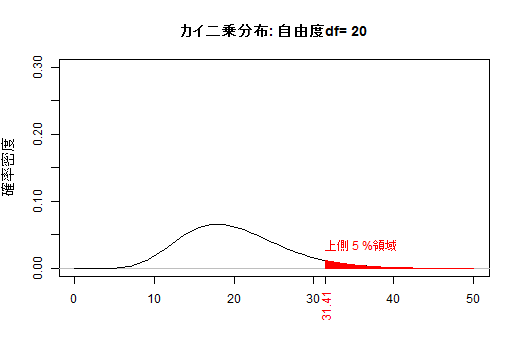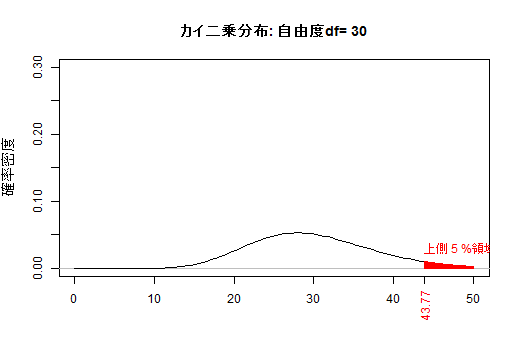
(b) 自由度によって変化するカイ二乗分布
自由度νのカイ二乗分布は,ν個の独立な標準正規変量の二乗和です。ν個の標準正規変量が一斉に0(または小さな絶対値)にならない限り,カイ二乗値は0(または小さな値)になりません。
(c) 標本サイズに応じて変化する二項分布
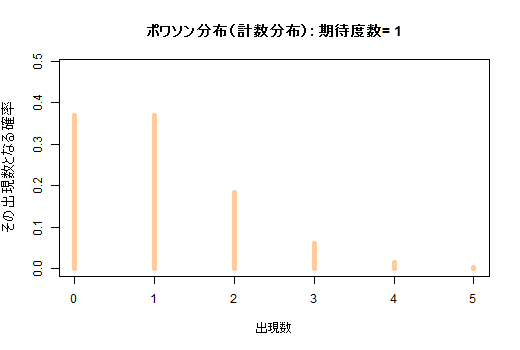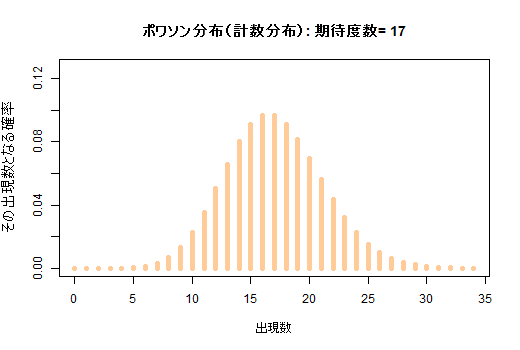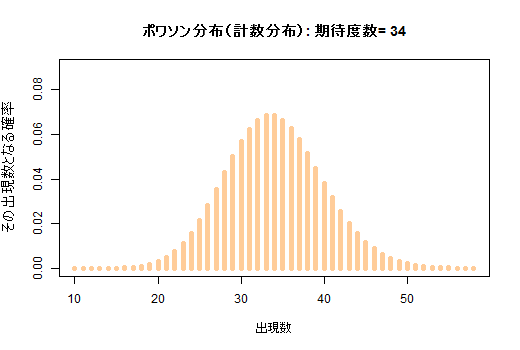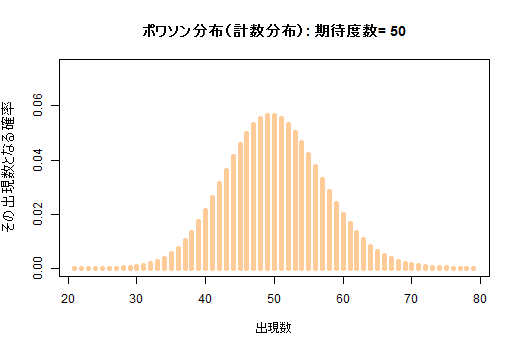
二項分布を元にしつつ,横軸で標本比率を表現したい為に比率に変換してあります。(d) 期待度数に応じて変化するポワソン分布
ポワソン分布では期待値と分散が等しくなります。余り明記してありませんが,クロス表のカイ二乗検定では,各セルがポワソン分布すると仮定してそれを標準化し,標準正規変量の二乗和としてカイ二乗値を計算しています。
期待度数が5未満だと,ポワソン分布が流石に正規分布で近似出来ないので不適切となると云う事です。
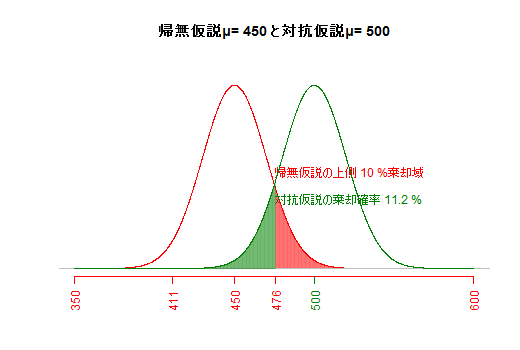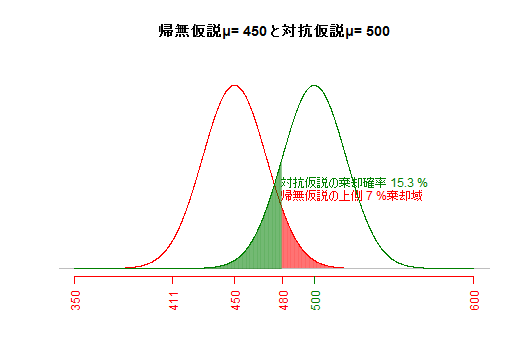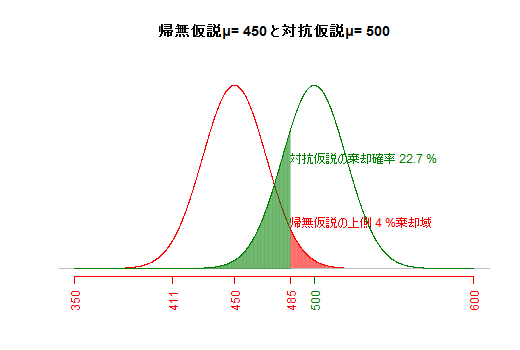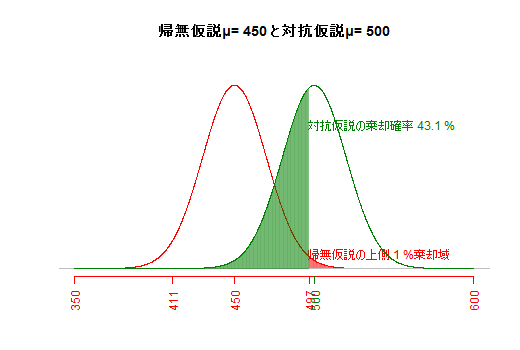
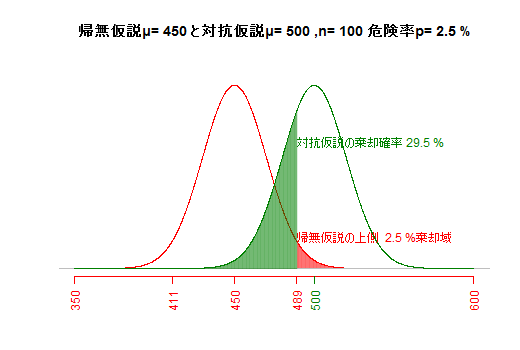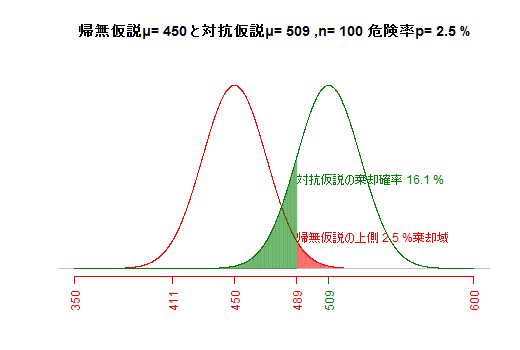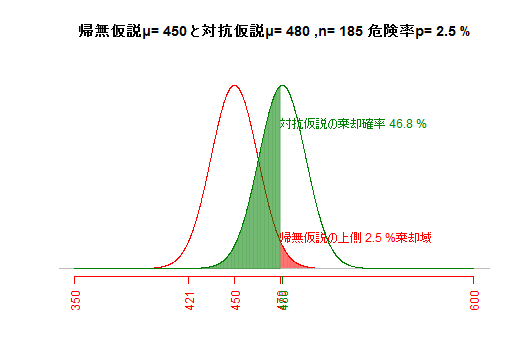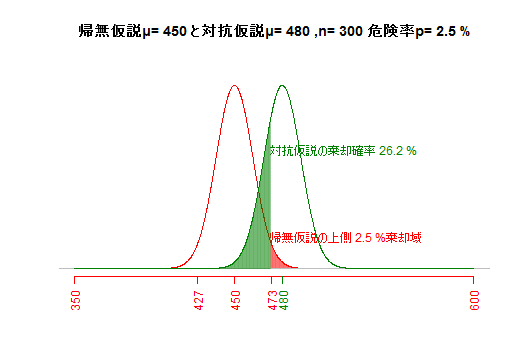
(e1) αエラー(第一種の過誤)とβエラー(第二種の過誤)
対抗仮説とサンプルサイズが一定の場合,危険率(αエラー,第一種の過誤)を小さくすると,βエラー(第二種の過誤;もし対抗仮説が正しかった場合に,対抗仮説が棄却されて帰無仮説が受容されてしまう誤り)が大きくなってしまう。(片側検定として図示)(e2) 仮説間の差の大きさとβエラー(第二種の過誤)
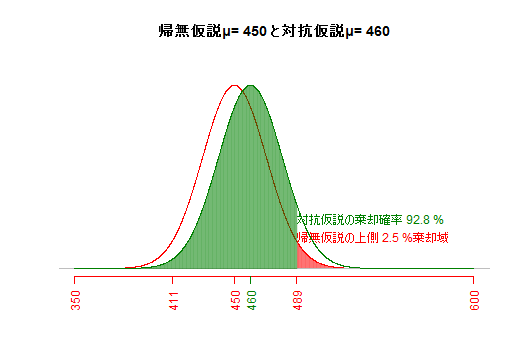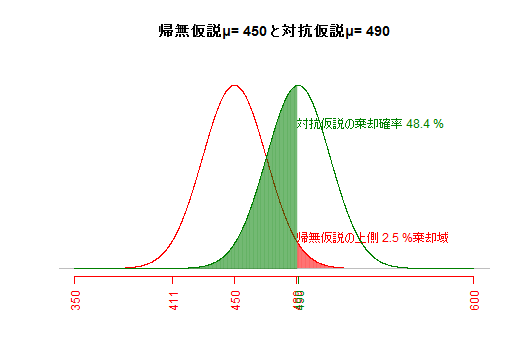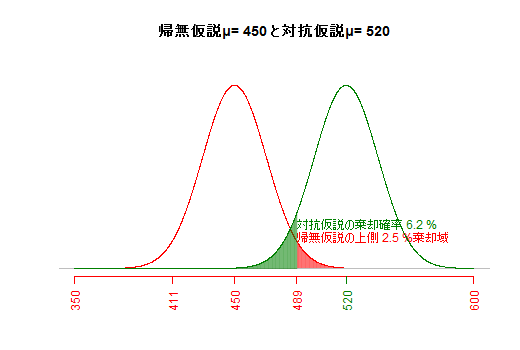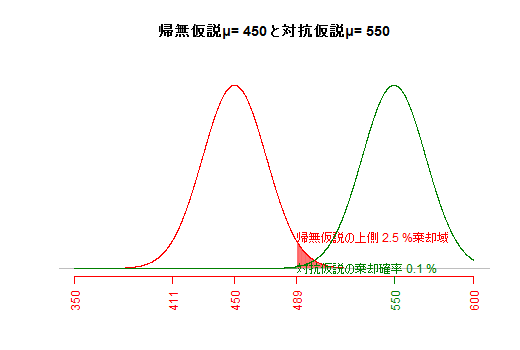
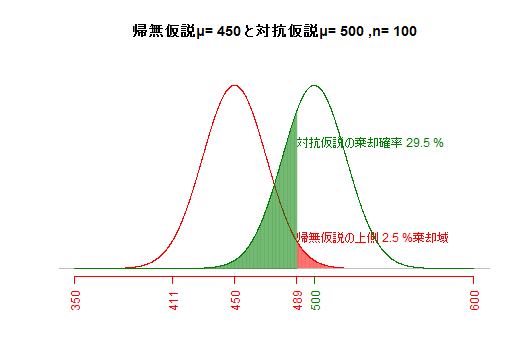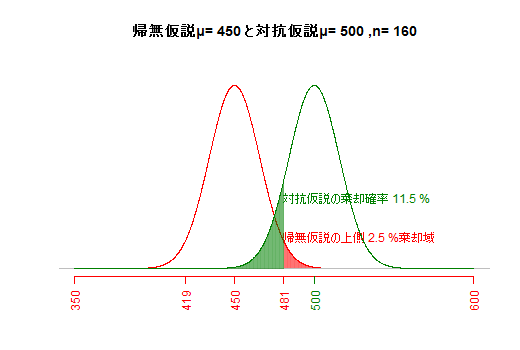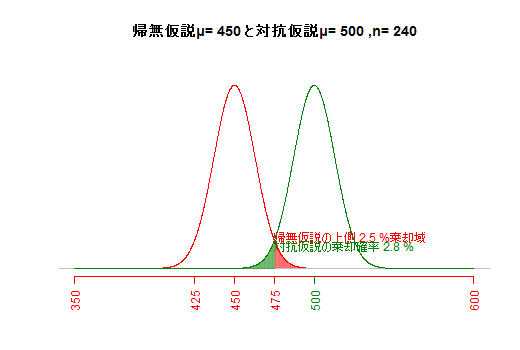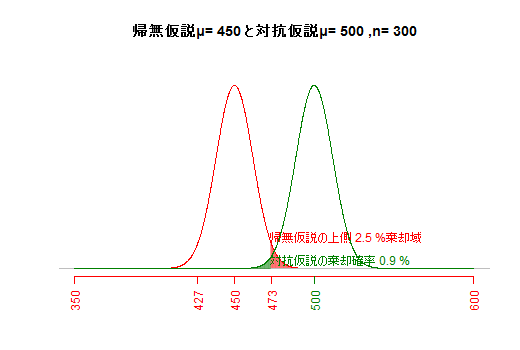
サンプルサイズと危険率が一定の場合,帰無仮説と対抗仮説が近いほど,βエラーが大きくなる。(e3) サンプルサイズとβエラー(第二種の過誤)
危険率と対抗仮説が一定の場合,サンプルサイズを大きくすれば標準誤差が小さくなり,βエラーが小さくなる。(e) βエラー(第二種の過誤)総合
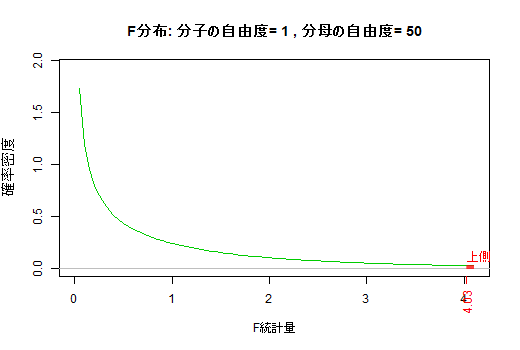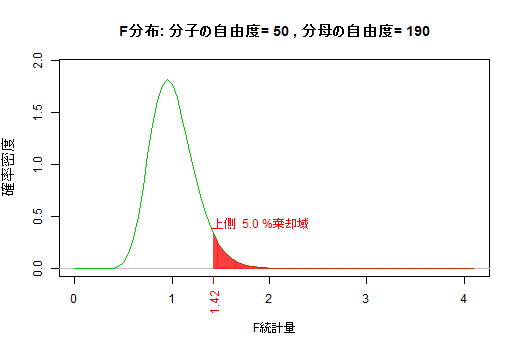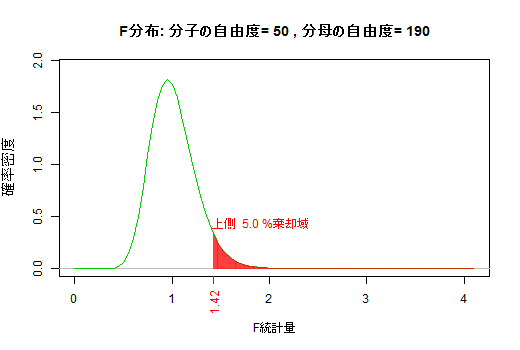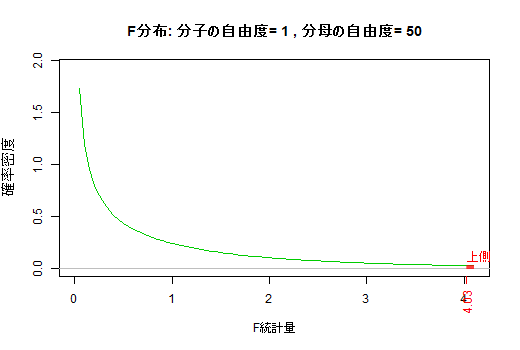
上記のe1, e2, e3のグラフを微調整の上,1つに統合しました。(f) F分布
F分布は二つの独立なカイ二乗統計量(をそれぞれ自由度で割ったもの)の比なので,分子と分母それぞれに自由度を持つ。社会統計学では分子の自由度の方が小さいものを扱うのが専らなので,その範囲で分子の自由度・分母の自由度を動かした時の5%棄却域を図示した。